https://www.acmicpc.net/problem/17070
17070번: 파이프 옮기기 1
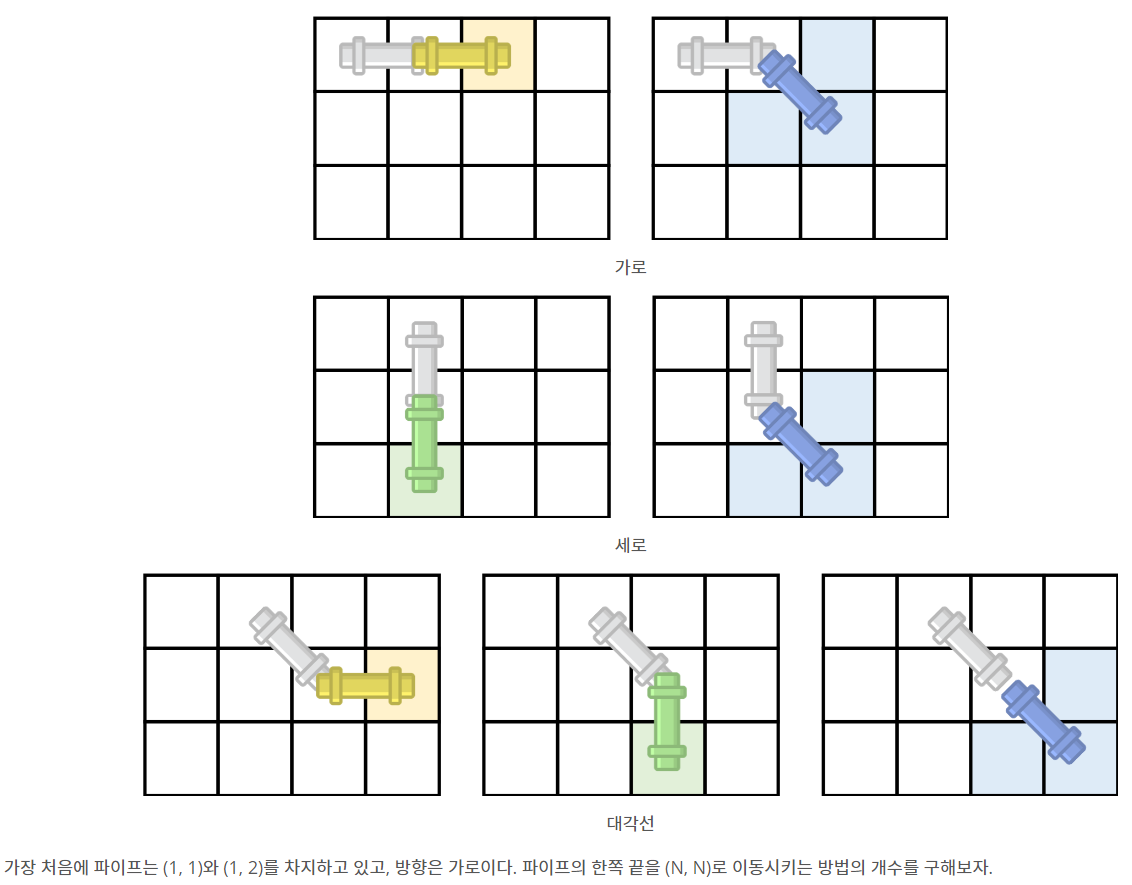
유현이가 새 집으로 이사했다. 새 집의 크기는 N×N의 격자판으로 나타낼 수 있고, 1×1크기의 정사각형 칸으로 나누어져 있다. 각각의 칸은 (r, c)로 나타낼 수 있다. 여기서 r은 행의 번호, c는 열의
www.acmicpc.net

증말증말 어려운 문제ㅠㅠ
처음에는 완전탐색으로 모든 모양을 돌리면서
만약에 ㅡ모양일 때 \ 모양을 (1,1)에서 두었다면 dp 배열에
x y 현재모양 다음모양
이런식으로 열을 만들어서 메모이제이션을 하려고 했었다. 그런데 구현하다가 이건 아닌 것 같아서 관둠
그래서 결국 다른 사람들의 도움을 받아.... 겨우 해결(이해)한 문제이다.
일단 dp를 쓰기 위해 배열을 어떻게 활용할 것인지 고민해야 한다.
기본 2차원 맵에 파이프를 놓는다고 할 때, 우리가 고려해야할 부분은 파이프가 가려는 위치이다.
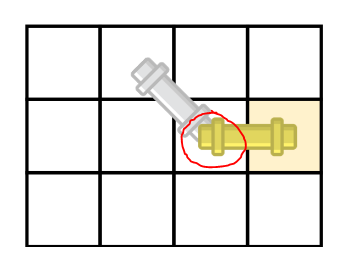
어떤 파이프를 밀더라도 저 부분에서 모든 일이 일어난다.
위 그림에서는 \ -> ㅡ 가 될 때 저 빨간 부분은 고정이고, 그 다음 위치가 y+1이 되는 것이다.
우리는 이제 저렇게 좌표 하나만 신경써주면 된다.
이제 여기서 중요함 아래 그림을 보자
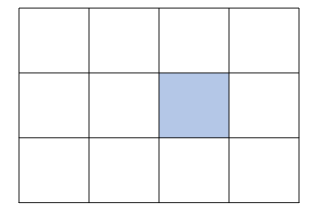
저 파란 부분에 도착했을 때 나올 수 있는 모양은 ㅡ | \ 이렇게 3가지가 있다.

그렇다면 이전 모양에 따라 올 수 있는 모양이 있으므로
저 파란 부분은 원래 어떤 모양이었을지 생각해봐야 한다.
만약에 저 파란 모양이 가로(ㅡ) 모양이었다면?

그 다음에 올 수 있는 모양은 가로와 대각선이 된다.

이렇게 생각해보면 문제에 나와있는 것처럼
| 이전 모양 | 나올 수 있는 모양 |
| 가로 | 가로, 대각선 |
| 세로 | 세로, 대각선 |
| 대각선 | 가로, 세로, 대각선 |
이렇게 가능해진다.
+ 대각선일 때에는 문제에서 보다시피 3칸이 필요하다.

그래서 애초에 이전 모양이 대각선이기 위해서는 저 노란 부분이 비어있어야 했다는 것을 꼭 처리해줘야 한다.
이제 어떻게 풀지는 알겠음
그러면 dp를 어떻게 만들까?
일단 map 위에서 모든 일이 일어날 것이므로 2차원 배열에, 우리가 저장해야할 것은 '모양'이 될 것이다.
현재 모양 += 이전 모양의 dp
그니까 이전 모양에서 올 수 있는 모양의 개수 합을 저장해놓고 그것을 계속 합해나가는 것이다.
코드
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
static int N, answer=0;
static int[][] map;
public static void main(String[] args) throws Exception{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
N = Integer.parseInt(br.readLine());
map = new int[N][N];
for(int i=0; i<N; i++) {
st = new StringTokenizer(br.readLine());
for(int j=0; j<N; j++)
map[i][j] = Integer.parseInt(st.nextToken());
}
///// 입력 끝 /////
int dp[][][] = new int[N][N][3]; // 3: 가로 세로 대각선
dp[0][1][0] = 1; // 처음 시작은 (0,1),가로 니까 010+=1
for(int i=0; i<N; i++) {
for(int j=2; j<N; j++) { // j=0,1일 때에는 아무것도 올 수 없으므로 모두 0이라 신경 안써도 된다.
if(map[i][j] == 1) continue;
// 가로
dp[i][j][0] += dp[i][j-1][0] + dp[i][j-1][2];
// 세로
if(i == 0) continue;
dp[i][j][1] += dp[i-1][j][1] + dp[i-1][j][2];
// 대각선
if(map[i][j-1] != 1 && map[i-1][j] != 1) {
dp[i][j][2] += dp[i-1][j-1][0] + dp[i-1][j-1][1] + dp[i-1][j-1][2];
}
}
}
System.out.println(dp[N-1][N-1][0] + dp[N-1][N-1][1] + dp[N-1][N-1][2]);
}
}
map에서 j=0,1일 때에는 어떤 모양이든 올 수 없으므로 0이라서 아예 신경쓰지 않아도 된다.
이전코드 (안봐도 됨)
원래 이렇게 짰었다.
for(int i=0; i<N; i++) {
for(int j=1; j<N; j++) {
if(i==0 && j==1) continue;
if(map[i][j] == 1) continue;
// 가로
dp[i][j][0] += dp[i][j-1][0] + dp[i][j-1][2];
// 세로
if(i == 0) continue;
dp[i][j][1] += dp[i-1][j][1] + dp[i-1][j][2];
// 대각선
if(map[i][j-1] != 1 && map[i-1][j] != 1) {
dp[i][j][2] += dp[i-1][j-1][0] + dp[i-1][j-1][1] + dp[i-1][j-1][2];
}
}
}
i==0, j==1일 때는 시작점이니까 넘어가고..음 저렇게 i==0일 때 continue; 하고... 어쩌구 이렇게 짰는데
위에꺼가 더 효율적이라고 해서 바꿨음

오우 골드5인데 너무 어렵네 dp.... 화이땡
'알고리즘 > 백준' 카테고리의 다른 글
| [BaekJoon] 백준 15644번 _ 구슬 탈출 3 for JAVA (0) | 2022.10.30 |
|---|---|
| [BaekJoon] 백준 13460번_구슬탈출 2 for JAVA (0) | 2022.10.30 |
| [BaekJoon] 백준 11053번_가장 긴 증가하는 부분 수열 for JAVA (0) | 2022.08.21 |
| [BaekJoon] 백준 2493번_탑 for JAVA (0) | 2022.08.07 |
| [BaekJoon] 백준 11866번 _ 요세푸스 문제 0.Python (0) | 2022.04.15 |