문제 1. 개미 전사


DP를 활용하여 문제를 풀 수 있다.
문제를 해결하기 위해 i번째 식량창고까지의 최적의 해를 살펴보자
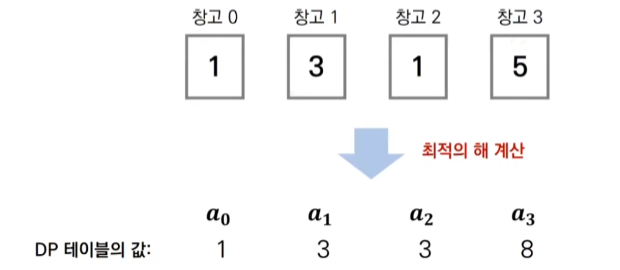
창고 0에서 최적의 해는 1이다.
창고 1에서 최적의 해는 1과 3을 비교했을 때 큰 값인 3이다.
창고 2에서 최적의 해는 1+1인 2와 3을 비교했을 때 큰 값인 3이다.
창고 4에서 최적의 해는 1+1인 2와 3+5인 8을 비교했을 때 큰 값인 8이다.
이런식으로 차례로 DP에 넣어 확인할 수 있다.
왼쪽부터 차례대로 식량창고를 털 때 i 번째를 털지 안털지의 여부는 2가지가 있다.

바로 앞의 창고가 털렸다면 i번째 창고는 털 수 없으며
털리지 않았다면 i번째 창고를 털 수 있다.

두 가지 중에 더 많은 식량을 털 수 있는 경우를 선택하면 된다.
글고 i - 1번째와 i - 2번째만 살펴보면 됨 i - 3부터는 그 이전에 경우를 고려해서 계산을 마쳐놨을텡께
코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class AntWorrier { // 개미전사 DP
public static void main(String[] args) throws IOException{
int warehouse[];
int d[] = new int[100];
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
warehouse = new int[N];
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
for(int i = 0; i < N; i++)
warehouse[i] = Integer.parseInt(st.nextToken());
d[0] = warehouse[0];
d[1] = Math.max(warehouse[0], warehouse[1]);
for(int i = 2; i < N; i++)
d[i] = Math.max(d[i - 1], d[i - 2] + warehouse[i]);
System.out.println(d[N - 1]);
}
}
출처 : https://www.youtube.com/watch?v=5Lu34WIx2Us&t=1495s
'알고리즘 > 자료구조와 알고리즘' 카테고리의 다른 글
| <문제> 효율적인 화폐 구성 (Dynamic Programming) (0) | 2022.02.21 |
|---|---|
| <문제> 1로 만들기 (Dynamic Programming) (0) | 2022.02.21 |
| [Algorithm] DP(Dynamic Programming) 다이나믹 프로그래밍 알고리즘 (0) | 2022.02.21 |
| [Algorithm] 순열(permutation) for JAVA (0) | 2022.02.17 |
| [Algorithm] BFS 알고리즘 (너비 우선 탐색) (0) | 2022.01.21 |